About Taxloop
The TAXLOOP project aims to fill remaining gaps in our knowledge about the largest known European tax fraud to date.
In October 2018 a cooperation between European journalists known as CORRECTIV documented the largest European tax fraud to date in the Cum-ex Files.
Cum-ex, and two related trading strategies known as cum-cum and cum-fake (henceforth cum-schemes) are schemes that allow investors to avoid paying the dividend-withholding tax (DWT), or to receive excessive tax reimbursements. The revenue loss in Europe is not yet known, but estimates suggest the damage exceeds €100 billion. Despite diligent reporting by journalists, there remain many gaps in our knowledge that can best be answered by our team of academic economists trained in econometrics and optimal taxation.
TAXLOOP aims to:
- Analyze which countries have been affected
- Quantify how much tax revenue has been lost
- Identify the key weaknesses in the tax code exploited by investors.
- Redesign the DWT tax framework in Europe
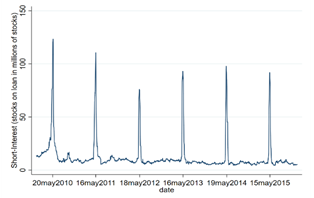 |
Figure 1 provides a concrete example of one of the schemes (cum-cum) in action. The figure displays the daily number of stocks on loan for BMW over time. As can be seen, lending spikes sharply every time BMW pays out a dividend. The reason is that foreign investors are lending their stocks to domestic banks, which are exempt from the DWT. |
|
After dividends are collected, the stocks return to the foreign investor, and the profits of not paying DWT are shared between the bank and the foreign investor. Propublica (2016) documents a similar trading pattern for most major German stocks. However, the schemes are not limited to Germany. All countries that levy a DWT, i.e. most EU-countries, are affected. Our aim is to map the impact of each of the cum-schemes across all of Europe, and to rigorously isolate fraudulent tax evasion schemes from regular trading patterns. To this end we will rely on high-quality data which we analyze by using state-of-the art econometrics and machine learning. This allows us to contribute in the fight against international tax evasion. |
|
 |
Floris T. Zoutman Project Manager/Principal Investigator |